
LESSON 4
Graphing Square Root Functions
Why?
With guitars, pitch is dependent on string
length and string tension. The longer the
string is, the higher the tension needs to
be to produce a desired pitch. Likewise,
the heavier the string is, the higher the
tension needs to be to reach a desired pitch.
This can be modeled by the square root
function
f
=
1
_
2
L
√
T
_
P
, where
T
is the tension,
P
is the mass of the string,
L
is the length
of the string, and
f
is the pitch.
Now
1
Graph square root
functions.
2
Analyze square root
functions.
Then
You simplified
expressions with
square roots.
New
Vocabulary
square root function
radical function
Mathematical
Practices
1
Make sense of
problems and persevere
in solving them.
2
Reason abstractly and
quantitatively.
4
Model with
mathematics.
1
Square Root Functions
If a function contains the square root of a variable, it is
called a
square root function
. The square root function is a type of
radical function
.
Key Concept
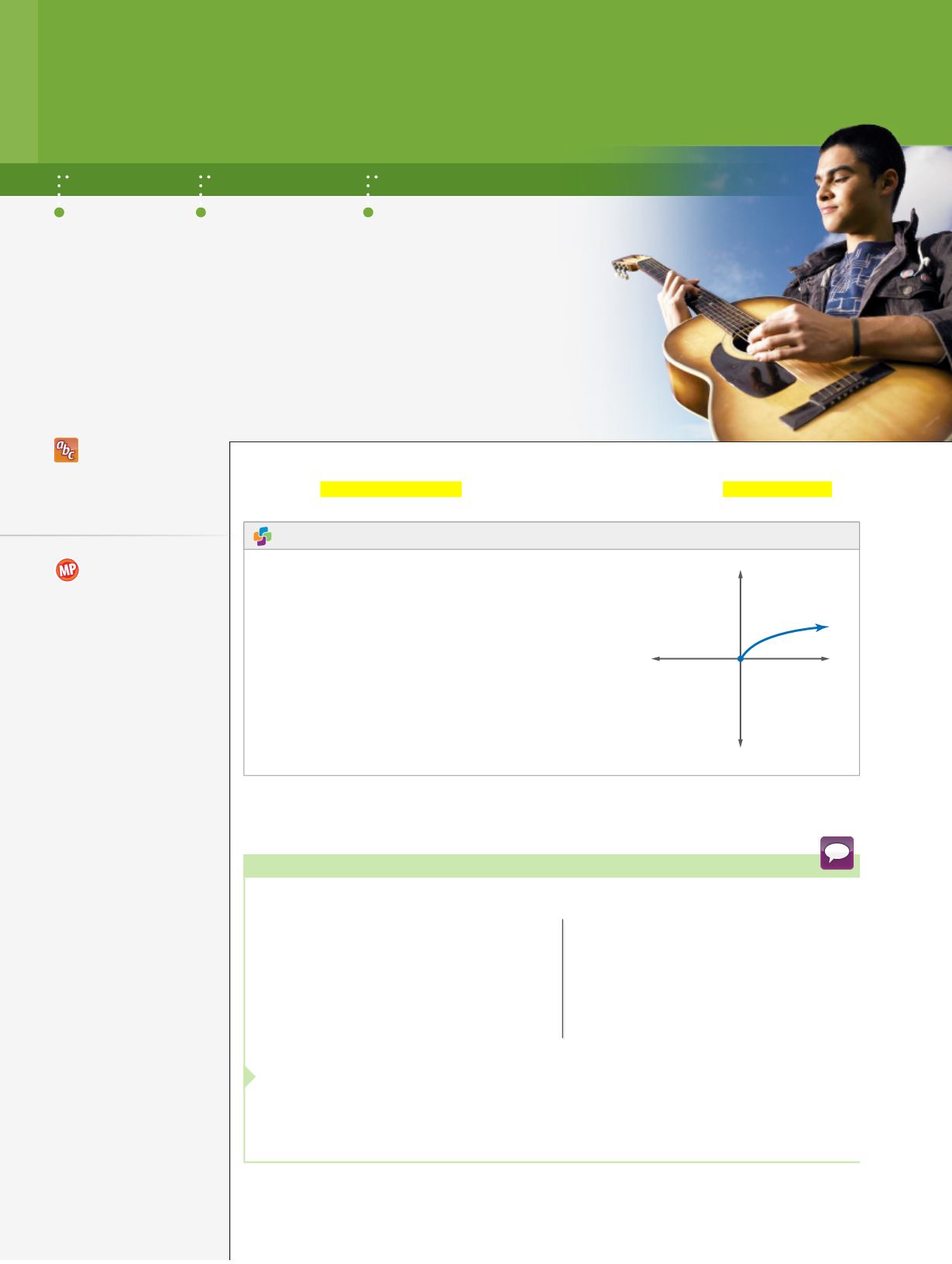
Parent Function of Square Root Functions
Parent function:
f
(
x
)
=
√
x
C07-010A-888482
x
≥
0
f
(
x
)
=
√
x
f
(
x
)
x
O
( 0, 0 )
Domain:
{
x
|
x
≥
0} or [0,
+∞
)
Range:
{
f
(
x
)
|
f
(
x
)
≥
0} or [0,
+∞
)
Intercepts:
x
=
0,
f
(
x
)
=
0
Symmetry:
none
Not defined:
x
<
0
End behavior:
x
→
0,
f
(
x
)
→
0;
x
→+∞
,
f
(
x
)
→+∞
Extrema:
minimum at (0, 0)
The domain of a square root function is limited to values for which the square root
function is defined.
Identify the domain and range of
f
(
x
)
=
√
x
+
4.
The domain only includes values for
Find
f
(
-
4) to determine the lower
limit of the range.
f
(
-
4)
=
√
-
4
+
4or 0
R
=
[0,
+∞),
{
f
(
x
)
|
f
(
x
)
≥
0},
or {0
≤
x
< ∞}
which the radicand is nonnegative.
x
+
4
≥
0
Write an inequality.
x
≥ -
4
Subtract 4 from each side.
D
=
[
-
4,
+∞),
{
x
|
x
≥ -
4},
or {
-
4
≤
x
< ∞}
.
Guided Practice
Identify the domain and range of each function.
1A.
f
(
x
)
=
√
x
-
3
1B.
f
(
x
)
=
√
x
+
6
+
2
Example 1
Identify Domain and Range
Ryan McVay/Lifesize/Getty Images
338
|
Lesson 5-4


















