
Find the inverse of the function. Then graph the function and its inverse on the same
coordinate plane.
31.
f
(
x
)
=
2
x
2
,
x
≥
0
32.
f
(
x
)
=
x
2
+
1,
x
≥
0
33.
f
(
x
)
= -
4
x
2
,
x
≥
0
34.
f
(
x
)
=
1
_
4
x
2
,
x
≥
0
35.
f
(
x
)
= -
1
_
2
x
2
,
x
≥
0
36.
f
(
x
)
=
4
x
2
+
2,
x
≥
0
37.
f
(
x
)
=
9
x
2
-
4,
x
≥
0
38.
f
(
x
)
=
3
_
4
x
2
+
8,
x
≥
0
39.
PHYSICS
The kinetic energy of an object is the energy produced due to its motion and
mass. The formula for kinetic energy, measured in joules
j
, is
E
=
0.5
mv
2
, where
m
is
the mass in kilograms and
v
is the velocity of the object in meters per second.
a.
Solve the above formula for
v
.
b.
If a 1500-kilogram vehicle is generating 1 million joules of kinetic energy, how fast is
it traveling?
c.
Escape velocity
is the minimum velocity at which an object must travel to escape the
gravitational field of a planet or other object. Suppose a ship that weighs 100,000
kilograms must have a kinetic energy of 3.624
×
10
14
joules to escape the
gravitational field of Jupiter. Estimate the escape velocity of Jupiter.
40.
REASONING
After an accident, police can determine how fast a car was traveling
before the driver put on his or her brakes by using the equation
v
=
√
30
fd
. In this
equation,
v
represents the speed in miles per hour,
f
represents the coefficient of
friction, and
d
represents the length of the skid marks in feet. The coefficient of
friction varies depending on road conditions. Assume that
f
=
0.6.
a.
Find the speed of a car that skids 25 feet.
b.
If your car is going 35 miles per hour, how many feet would it take you to stop?
c.
If the speed of a car is doubled, will the skid be twice as long? Explain.
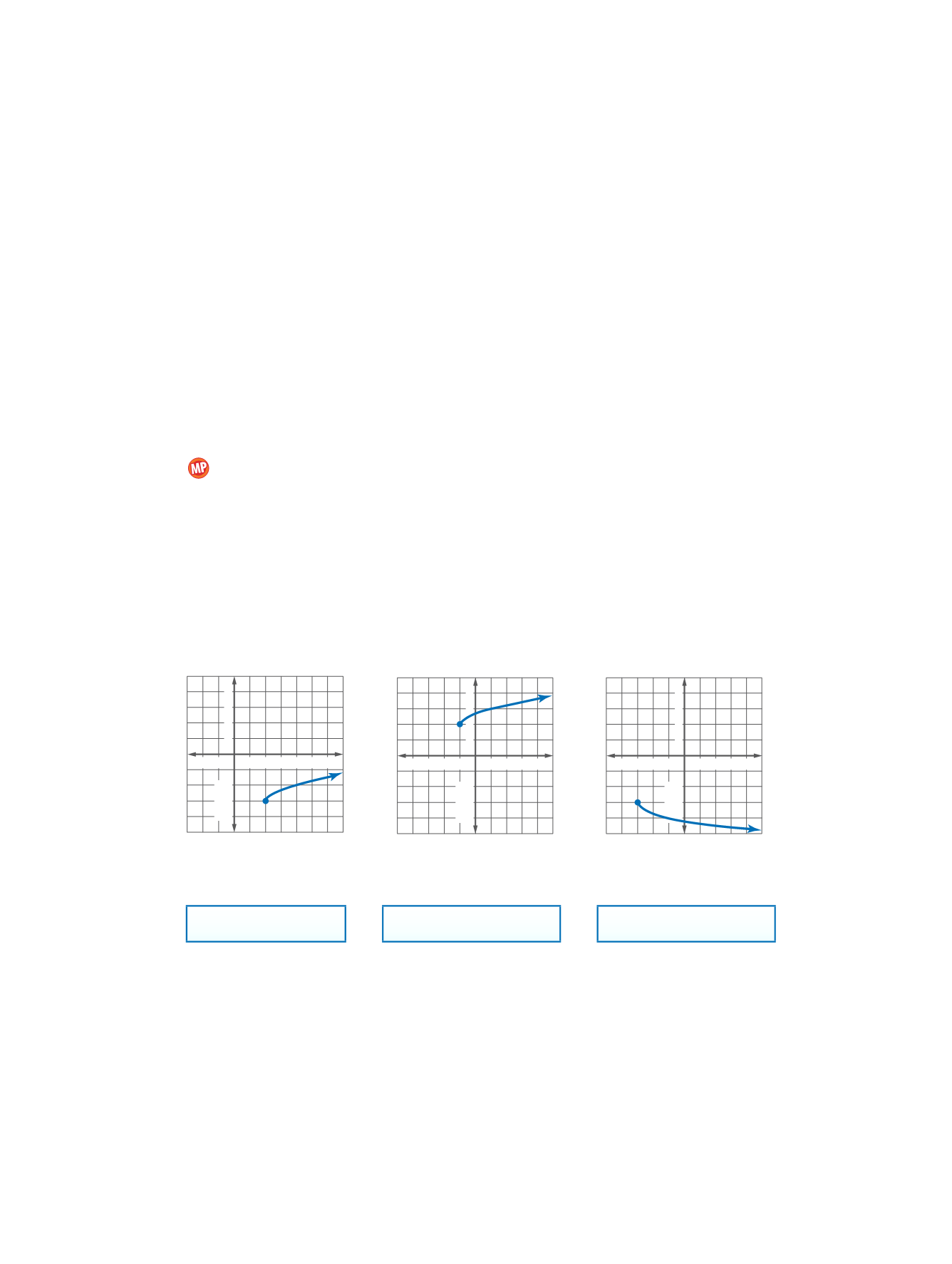
Write the square root function represented by each graph.
41.
42.
43.
C07-015A-888482
x
2 4 6 8 12 10
−
4
8
6
4
2
y
−
2
−
4
−
6
−
8
O
C07-016A-888482
x
2 4 86
−
8
−
6
−
4
8
6
4
2
y
−
2
−
4
−
6
−
8
O
C07-017A-888482
x
2 4 86
−
8
−
6
−
4
8
6
4
2
y
−
2
−
4
−
6
−
8
O
44.
REASONING
In this problem, you will use the following functions to investigate
transformations of square root functions.
f
(
x
)
=
4
√
x
-
6
+
3
g
(
x
)
=
√
16
x
+
1
-
6
h
(
x
)
=
√
x
+
3
+
2
a. Graphical
Graph each function on the same set of axes.
b. Analytical
Identify the transformation on the graph of the parent function. What
values caused each transformation?
c. Analytical
Which functions appear to be stretched or compressed vertically?
Explain your reasoning.
d. Verbal
The two functions that are stretched appear to be stretched by the same
magnitude. How is this possible?
e. Tabular
Make a table of the rate of change for all three functions between 8 and 12
as compared to 12 and 16. What generalization about rate of change in square root
functions can be made as a result of your findings?
Example 4
342
|
Lesson 5-4
|
Graphing Square Root Functions


















