
Check Your Understanding
=
Step-by-Step Solutions begin on page R14.
Identify the domain and range of each function. Describe the attributes of the graph.
1.
f
(
x
)
=
3
√
x
-
4
2.
f
(
x
)
=
3
√
x
+
2
-
3
3.
f
(
x
)
=
2
3
√
x
-
6
Graph each function. State key features of the graph.
4.
f
(
x
)
=
3
√
x
+
2
5.
f
(
x
)
=
2
3
√
x
-
1
6.
f
(
x
)
=
1
_
2
3
√
x
+
2
-
3
7.
f
(
x
)
= -
3
3
√
x
-
4
+
4
8.
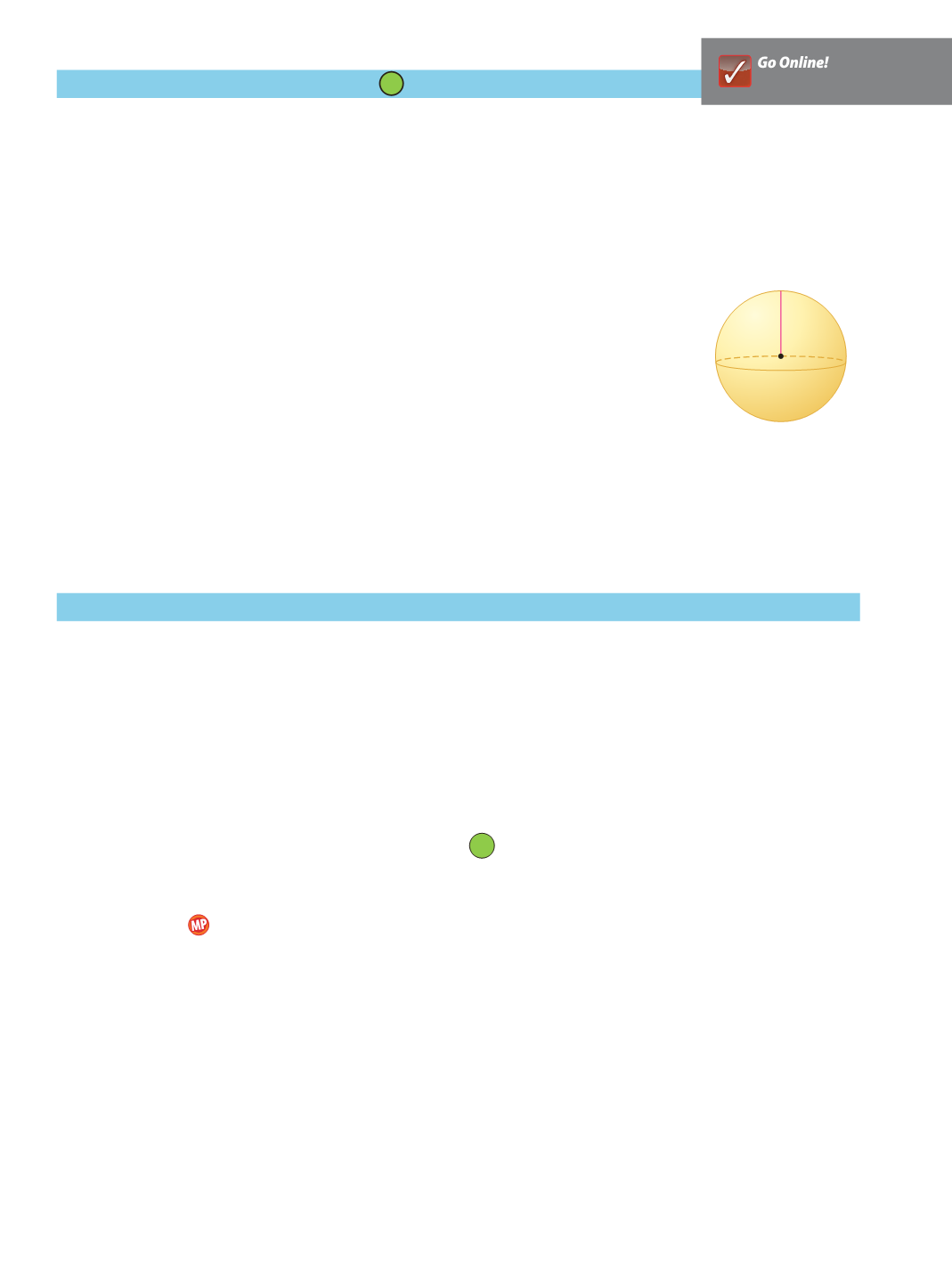
GEOMETRY
The radius
r
of a sphere with volume
V
can be found using the formula
r
=
3
√
3
V
_
4
π
.
a.
Graph the function.
b.
Use the graph to determine the approximate radius for volumes of
1000 cubic meters, 8000 cubic meters, and 64,000 cubic meters.
c.
How does the volume of the sphere change if the radius is doubled? Explain.
Find the inverse of the function. Then graph the function and its inverse on the same
coordinate plane.
9.
f
(
x
)
=
2
x
3
10.
f
(
x
)
=
x
3
+
1
11.
f
(
x
)
= -
4
x
3
12.
f
(
x
)
=
1
_
2
x
3
Practice and Problem Solving
Extra Practice is on page R5.
Identify the domain and range of each function. Describe the attributes of the graph.
13.
f
(
x
)
=
2
3
√
x
+
4
14.
f
(
x
)
= -
1
_
4
3
√
x
+
1
15.
f
(
x
)
=
1
_
3
3
√
x
-
2
+
1
Graph each function. State key features of the graph.
16.
f
(
x
)
=
3
√
x
-
3
17.
f
(
x
)
=
3
3
√
x
+
1
18.
f
(
x
)
=
1
_
4
3
√
x
-
1
-
4
19.
f
(
x
)
= -
3
√
x
+
1
-
2
20.
f
(
x
)
=
2
3
√
x
+
3
21.
f
(
x
)
=
3
3
√
x
+
2
-
4
22.
f
(
x
)
=
1
_
2
3
√
x
-
3
+
1
f
(
x
)
= -
2
3
√
x
-
4
-
2
24.
f
(
x
)
=
1
_
3
3
√
x
-
1
25.
f
(
x
)
=
1
_
2
3
√
x
-
2
+
2
26.
PERSERVERANCE
The radius
r
of the orbit of a communications satellite is given by
r
=
3
√
GMt
2
_
4
π
2
,
where
G
is the universal gravitational constant,
M
is the mass of Earth, and
t
is the
time it takes the satellite to complete one orbit. Find the radius of the satellite’s orbit if
G
is 6.67
×
10
-
11
N
·
m
2
/kg
2
,
M
is 5.98
×
10
24
kilograms, and
t
is 2.6
×
10
6
seconds.
27.
MODELING
A fruit grower has found that the circumference
C
, in inches, of most of his fruit crop
can be modeled by the cube root equation
C
=
3
√
W
_
0.009
, where
W
is the weight in ounces.
a.
Graph the function.
b.
What is the approximate circumference of a piece of fruit that weighs 8.5 ounces?
c.
What is the approximate weight of a piece of fruit with a circumference of 8 inches?
d.
Explain why it is difficult to give a function that will work on all fruit.
Example 1
Example 2
Example 3
Example 4
Example 1
Example 2
23
for a
Self-Check Quiz
C07-021A-888482
r
348
|
Lesson 5-5
|
Graphing Cube Root Functions


















