
The same techniques used to transform the graph of other functions you have studied can
be applied to the graphs of cube root functions.
Key Concept
Transformations of Cube Root Functions
f
(
x
)
=
a
3
√
x
-
h
+
k
Inflection Point (
h, k
)
h
—Horizontal Translation
h
units right if
h
is positive
⎜
h
⎟
units left if
h
is negative
The domain is all real numbers.
k
—Vertical Translation
k
units up if
k
is positive
⎜
k
⎟
units down if
k
is negative
The range is all real numbers.
a
—Orientation and Shape
• If
a
<
0, the graph is reflected across the
x
-axis.
• If
⎜
a
⎟
>
1, the graph is stretched vertically.
• If 0
<
⎜
a
⎟
<
1, the graph is compressed vertically.
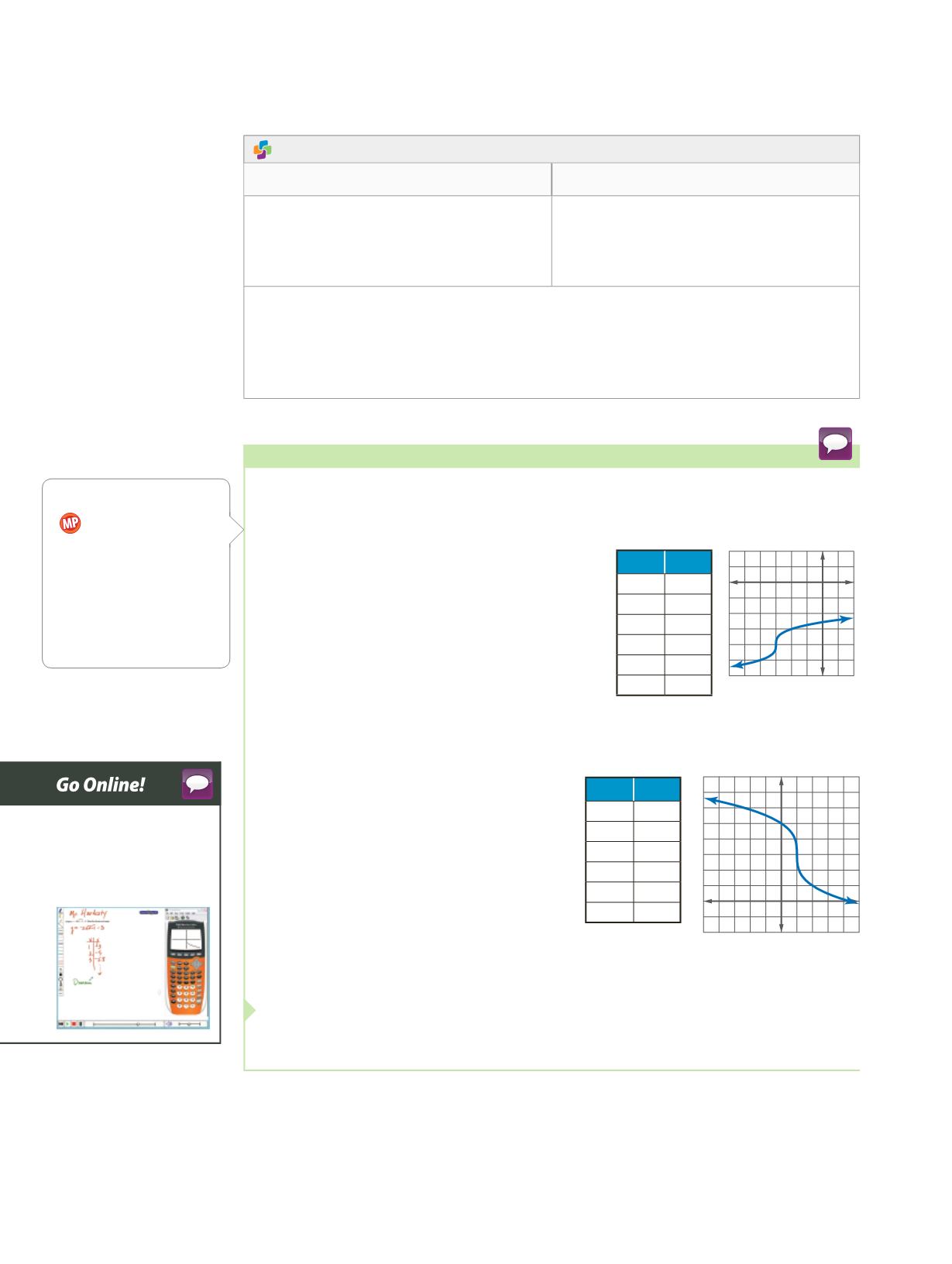
Graph each function. State key features of the graph.
a.
y
=
3
√
x
+
3
-
4
Make a table of values and graph the function.
The graph is the same shape as
f
(
x
)
=
3
√
x
, but
is translated 3 units to the left and 4 units
down.
Domain and Range:
D
=
{
x
| -∞ <
x
< +∞
} or (
-∞
,
+∞
)
R
=
{
f
(
x
)
| -∞ <
f
(
x
)
< +∞
} or (
-∞
,
+∞
)
End behavior: The value of
y
increases as the
value of
x
increases. Inflection point: (
h
,
k
)
=
(
-
3, 4)
b.
y
= -
2
3
√
x
-
1
+
3
Make a table of values and graph the
function. The graph of
f
(
x
)
=
3
√
x
is
stretched by a factor of 2, translated 1
unit to the right, 3 units up, and reflected
in the line
x
=
1.
Domain and Range:
D
=
{
x
| -∞ <
x
< +∞
} or (
-∞
,
+∞
)
R
=
{
f
(
x
)
| -∞ <
f
(
x
)
< +∞
} or (
-∞
,
+∞
)
End behavior: The value of
y
decreases as the
value of
x
increases. (
h
,
k
)
=
(1, 3)
Guided Practice
2A.
y
=
3
√
x
-
3
+
2
2B.
y
= -
3
3
√
x
+
1
-
2
Example 2
Graph Cube Root Functions
2
Analyze Cube Root Functions
Previously you learned that an inverse relation
interchanges the
x
- and
y
-coordinates of the original relation. For the power function
f
(
x
)
=
x
3
, the inverse of
f
is the function
f
-
1
(
x
)
=
3
√
x
for all real numbers.
Follow along with your
graphing calculator as you
watch a
Personal Tutor
graph a square root
function.
x
y
-
4
-
5
-
3
-
4
-
2
-
3
0
-
2.6
2
-
2.3
5
-
2
x
y
-
7
7
-
1
5.5
0
5
1
3
2
1
3
0.5
C05_020A_903990
y
x O
C05_021A_903990
y
x
O
Teaching Tip
Reason Abstractly
Encourage students to
compare the transformations
of a cube root function with
transformations of a square
root function. Have them
explain to each other the
similarities and differences.
346
|
Lesson 5-5
|
Graphing Cube Root Functions


















