
Michael Krabs/Imagebroker RF/Getty Images
NATURE
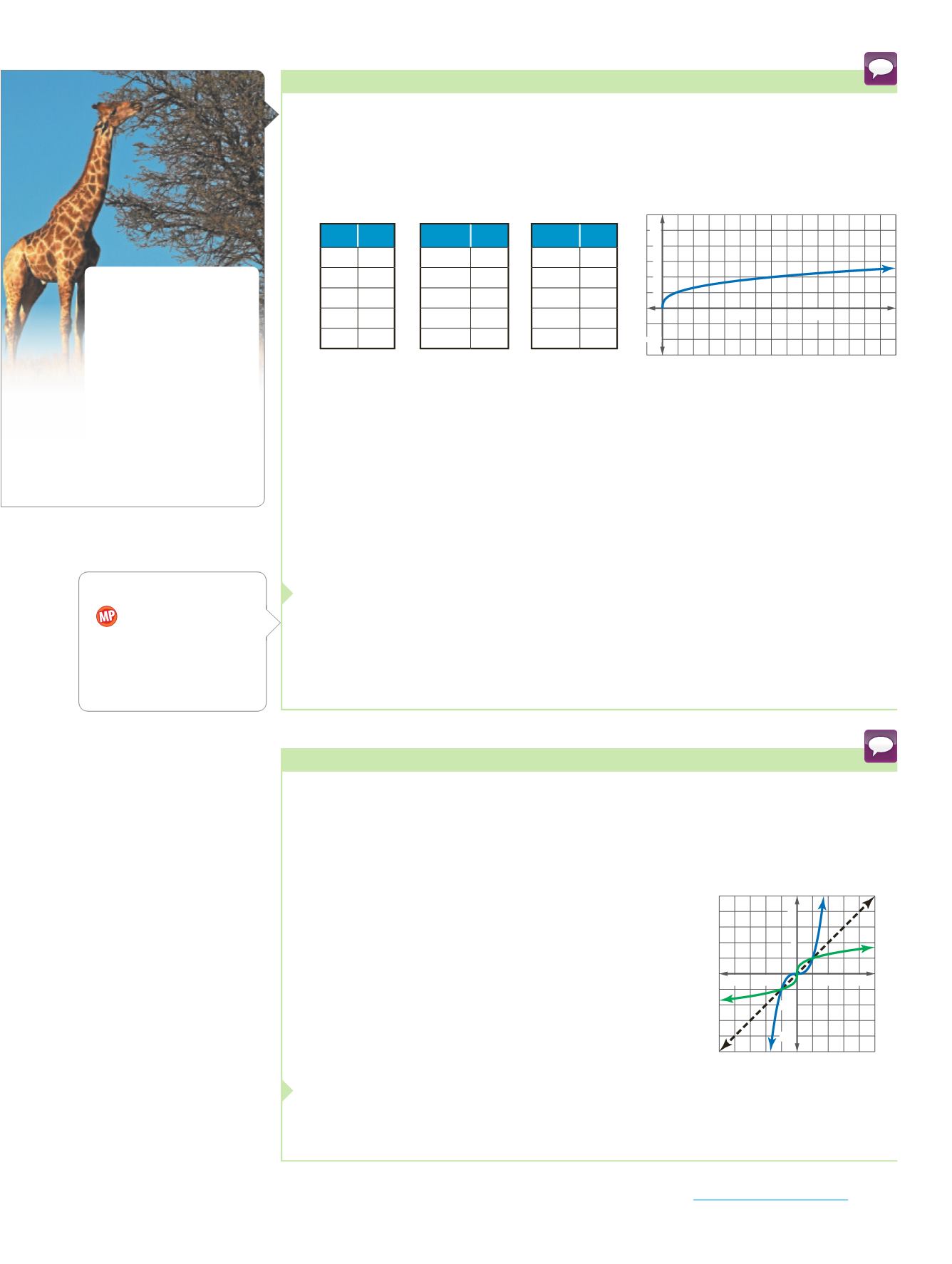
Refer to the application at the beginning of the lesson. A zookeeper found
that the height of some small giraffes weighing
x
kilograms can be modeled by the
cube root function
h
(
x
)
=
0.45
3
√
x
, where
h
is the height in meters.
a.
Make a table and graph the function in the domain {
x
|
0
≤
x
≤
1500}.
Round output values to the nearest tenth.
x
h
600 3.8
700 4.0
800 4.2
900 4.3
1000 4.5
x
h
1100 4.6
1200 4.8
1300 4.9
1400 5.0
1500 5.2
x h
0 0
200 2.6
300 3.0
400 3.3
500 3.6
b.
Analyze the graph. How should the domain be restricted?
The domain should be restricted to be between about 700 to 1300 kilograms,
because that is the approximate weight range for giraffes.
c.
What are key features of the graph?
The graph is in the first quadrant only. The values of
y
increase as the values of
x
increase.
d.
What is the approximate height of a giraffe that weighs 850 kilograms?
According to the graph and the table, the height is about 4.26 meters.
Guided Practice
3.
The height of some larger giraffes weighing
x
kilograms is better modeled by the
cube root function
h
(
x
)
=
0.55
3
√
x
, where
h
is the height in meters. Graph the
function in the domain {
x
|
0
≤
x
≤
1300} and analyze the graph. Then determine
the approximate height of a giraffe that weighs 1150 kilograms.
Real-World Example 3
Use Graphs to Analyze Cube Root Functions
Find the inverse of
f
(
x
)
=
x
3
. Then graph
f
(
x
) and
f
-
1
(
x
) on the same coordinate plane.
f
(
x
)
=
x
3
Write the original function.
y
=
x
3
Replace
f
(
x
) with
y
.
x
=
x
3
Interchange
x
and
y
.
3
√
x
=
y
Take the cube root of both sides.
Because the domain of
f
is all real numbers, the range
of
f
–1
is also all real numbers. So, the inverse of
f
is
f
–1
(
x
)
=
3
√
x
with domain and range all real numbers.
The graph of
f
–1
(
x
)
=
3
√
x
is a reflection of the graph of
f
(
x
)
=
x
3
in the line
y
=
x
, shown as a dashed line on
the graph.
Guided Practice
4.
Find the inverse of
f
(
x
)
=
x
3
-
1. Then graph
f
(
x
) and
f
–1
(
x
) on the same coordinate
plane.
Example 4
Find the Inverse of Power Function
f
(
x
)
=
x
3
C05_022A_903990
6
4
2
500
1000
8
10
y
x
O
−
4
Real-World Link
As the world’s tallest
mammals, giraffes use their
height for reaching the
leaves of tall trees, and their
long legs to help them run
as fast as 35 miles per hour
for short distances. For
longer distances, they run
10 miles per hour.
Source:
http://animals.
nationalgeographic.c om/animals/
mammals/giraffe/
Problem-Solving Tip
Modeling
Making a
table is a good way to
organize ordered pairs in
order to see the general
behavior of a graph.
C05_023A_903990
−
2
−
1
2 1
−
2
−
1
2
1
y
x
O
connectED.mcgraw-hill.com347


















