
LESSON 1
Operations with Functions
1
Perform Operations with Functions
You have performed arithmetic operations
with polynomials. You can also use addition, subtraction, multiplication, and division
with functions.
You can perform arithmetic operations according to the following rules.
Key Concept
Operations on Functions
Operation
Definition
Example
Let
f
(
x
)
=
2
x
and
g
(
x
)
=-
x
+
5.
Addition
(
f
+
g
)(
x
)
=
f
(
x
)
+
g
(
x
)
2
x
+
(
-
x
+
5)
=
x
+
5
Subtraction
(
f
-
g
)(
x
)
=
f
(
x
)
-
g
(
x
)
2
x
-
(
-
x
+
5)
=
3
x
-
5
Multiplication
(
f
·
g
)(
x
)
=
f
(
x
)
·
g
(
x
)
2
x
(
-
x
+
5)
= -
2
x
2
+
10
x
Division
(
f
_
g
)
(
x
)
=
f
(
x
)
_
g
(
x
)
,
g
(
x
)
≠
0
2
x
_
-
x
+
5
,
x
≠
5
Given
f
(
x
)
=
x
2
-
4 and
g
(
x
)
=
2
x
+
1, find each function.
a.
(
f
+
g
)(
x
)
(
f
+
g
)(
x
)
=
f
(
x
)
+
g
(
x
)
Addition of functions
=
(
x
2
-
4)
+
(2
x
+
1)
f
(
x
)
=
x
2
-
4 and
g
(
x
)
=
2
x
+
1
=
x
2
+
2
x
-
3
Simplify.
b.
(
f
-
g
)(
x
)
(
f
-
g
)(
x
)
=
f
(
x
)
-
g
(
x
)
Subtraction of functions
=
(
x
2
-
4)
-
(2
x
+
1)
f
(
x
)
=
x
2
-
4 and
g
(
x
)
=
2
x
+
1
=
x
2
-
2
x
-
5
Simplify.
Guided Practice
Given
f
(
x
)
=
x
2
+
5
x
-
2 and
g
(
x
)
=
3
x
-
2, find each function.
1A.
(
f
+
g
)(
x
)
1B.
(
f
-
g
)(
x
)
Example 1
Add and Subtract Functions
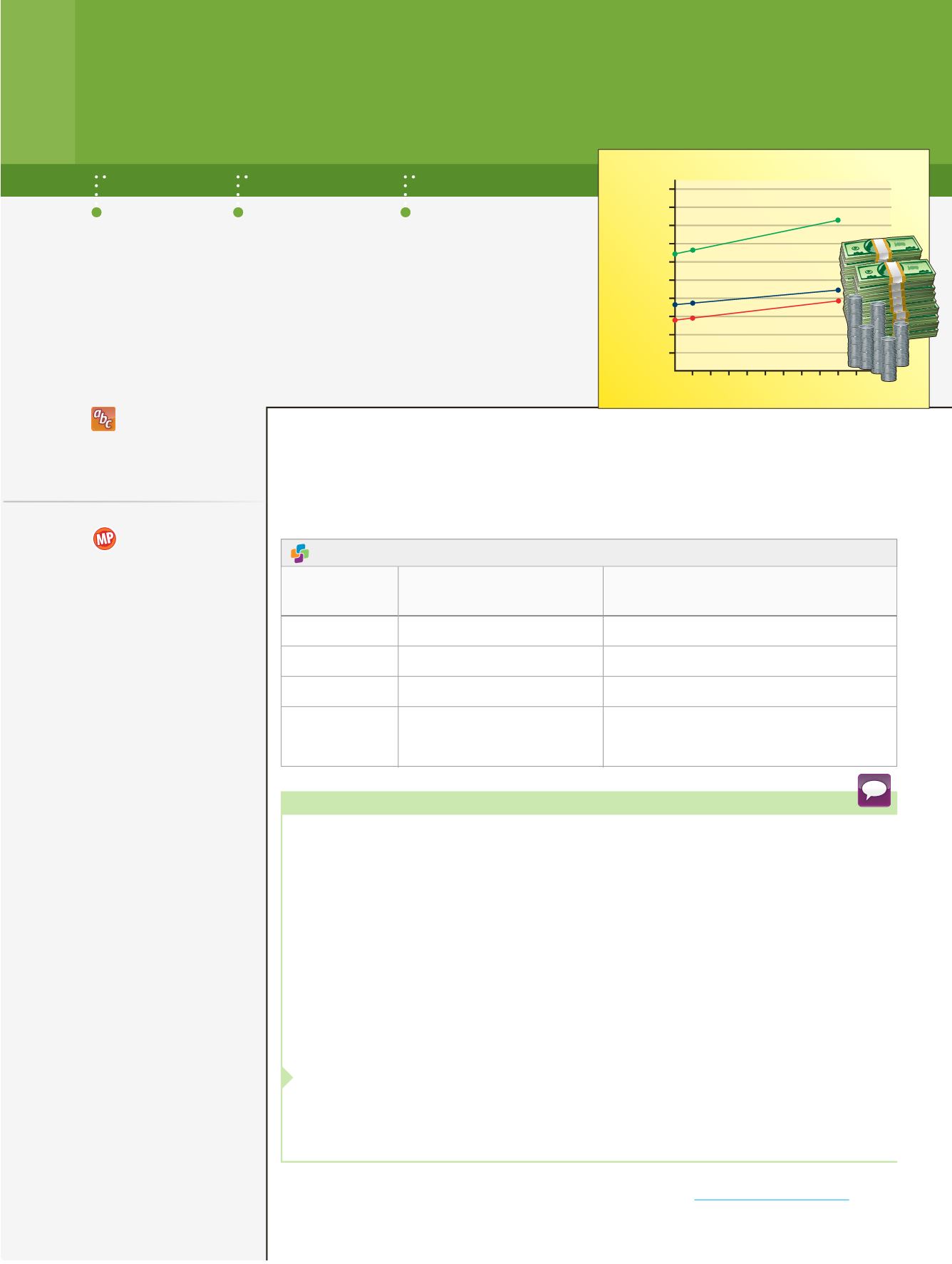
Why?
The graphs model the income
for the Brooks family since
2005, where
m
(
x
) represents
Mr. Brooks’ income and
f
(
x
)
represents Mrs. Brooks’ income.
The total household income for
the Brooks household can be
represented by
f
(
x
)
+
m
(
x
).
Now
1
Perform arithmetic
operations with
functions.
2
Apply arithmetic
operations with
functions.
Then
You performed
operations on
polynomials.
New
Vocabulary
composition of
functions
Mathematical
Practices
4
Model with
mathematics.
7
Look for and make use
of structure.
10,000
0
20,000
30,000
40,000
50,000
60,000
70,000
80,000
90,000
100,000
m(x)
+
f(x)
f(x)
m(x)
2
Years Since 2005
Income ($)
4 6 8 10
Brooks Household Income
C07-001A-88482-B
connectED.mcgraw-hill.com315


















