
Get Ready
for the Chapter
English
Español
composition of functions
p. 322
composición de funciones
inverse relation
p. 329
relaciones inversas
inverse function
p. 329
función inversa
square root function
p. 338
función raíz cuadrada
radical function
p. 338
función radical
cube root function
p. 345
función ráiz cúbica
inflection point
p. 345
punto de inflexión
radical equation
p. 352
ecuación radical
extraneous solution
p. 352
solución extraña
radical inequality
p. 354
desigualdad radical
absolute value
valor absoluto
a number’s distance from zero
on the number line, represented by
⎜
x
⎟
C01-019A-888482
5
5
432 1
4 3 2 1 0
4 units
4 units
rational number
número racional
any number
m
_
n
, where
m
and
n
are integers and
n
is not zero; the decimal form is either
a terminating or repeating decimal.
relation
relación
a set of ordered pairs
Concept Check
Review the concepts used in this chapter by answering
the questions below.
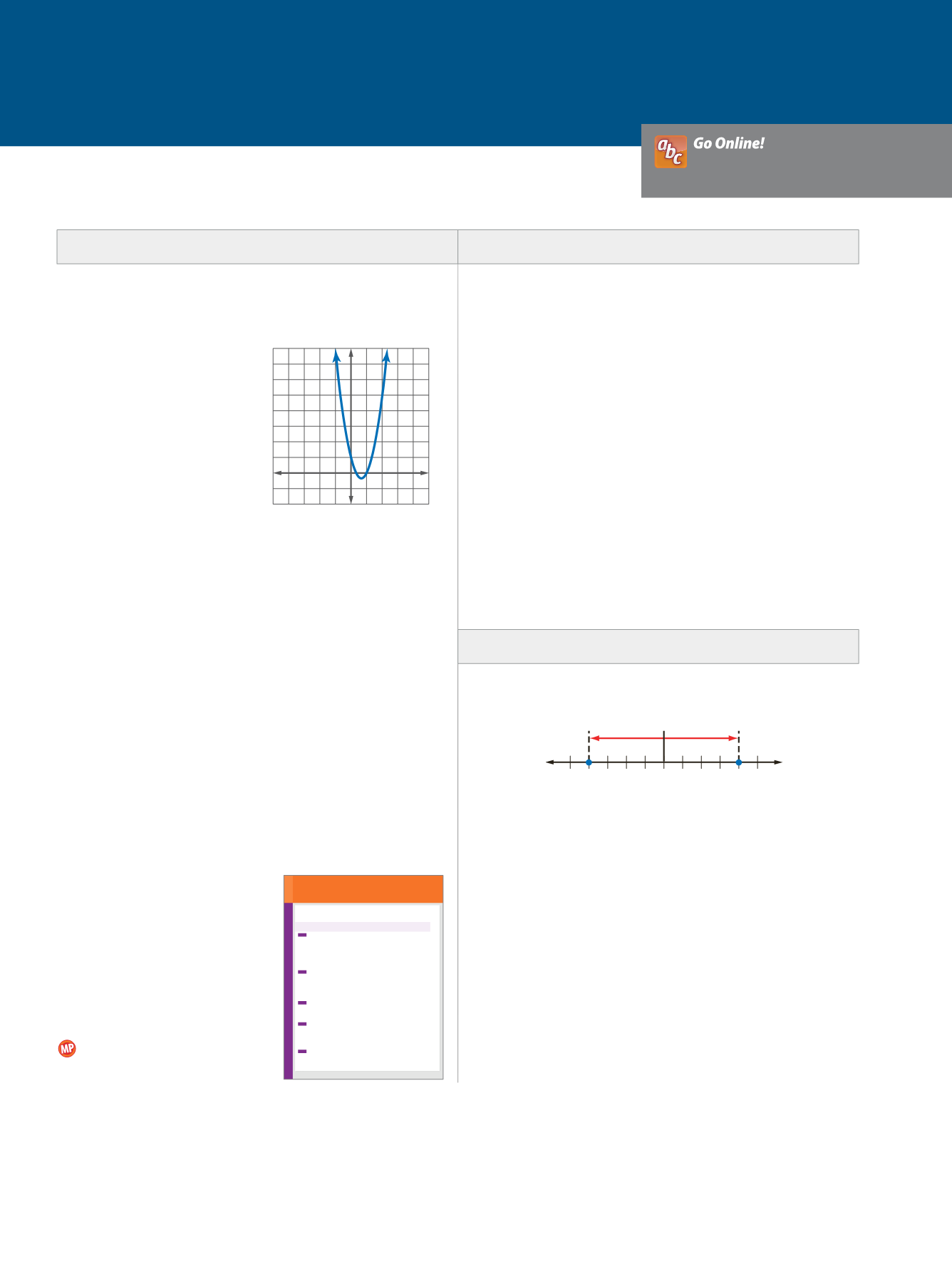
1.
In a graph such as the one
shown, how do you define
the “roots” of the graph?
2.
If the exact roots of a graph
cannot be found, what is
typically stated?
3.
What are the roots of the
graph shown?
4.
What type of division would you use to simplify
(5
x
2
-
22
x
-
15)
÷
(
x
-
5)?
5.
What property would you use to rewrite
-
1
_
2
(2
m
-
5)
without parentheses?
6.
Given
=
3
x
2
+
3
x
-
5
x
-
5, what property can you
apply to begin to simplify the equation?
7.
Given
=
3
x
(
x
+
1)
-
5(
x
+
1), what property can you
apply to simplify the equation?
8.
How would
-
1(3
b
2
+
2
b
-
1) be written so that it does
not contain parentheses?
9.
Given 4
x
2
+
7
x
+
3, what are the values for
a
,
b
, and
c
when applying the Quadratic Formula?
10.
Given
3
m
+
5
n
_
p
, where
m
= -
5,
n
=
2, and
p
= -
1,
would you have a positive or negative number?
Performance Task Preview
You can use the concepts and skills
in the chapter to perform various
calculations on data collected in a
university lab. Understanding
inverses and radical functions will
help you finish the Performance
Task at the end of the chapter.
In this Performance Task
you will:
• make sense of problems and
persevere in solving them
• reason abstractly and quantitatively
• attend to precision
CHAPTER5
Preparing forAssessment
PerformanceTask
Provideaclearsolution toeachpartof the task.Besure toshowallofyourwork, includeall
relevantdrawings,and justifyyouranswers.
PartA
Afterstudyingproductionof twodifferentvarietiesof tomatoesgrown in two identical
gardens,Ravicomesupwith the followingequations torepresent the tomatoes’productionrates:
VarietyA:
t
=
2
d
2
+
4
d
-
2 VarietyB:
t
=
d
2
+
d
+
1
InRavi’smodels,
t
represents the totalnumberof tomatoesproduced ineachgardenand
d
represents thenumberofwholedays since theplants first startedproducing tomatoes.
• Writeanexpression thatmodels the totalproduction ratesofboth varieties.
• Determinewhich variety ismoreproductive.Explain your reasoning.
• Writeanexpression thatmodelshowmuchmoreproductive
one variety is than theother.
PartB
While studying thedeclineofacertainkindofcell inchildrenwithcertain illnesses,
Ravicalculates the following functions to representhow thedecrease in thenumbersofcells
c
asa functionof thenumberofdays
d
thechildhas the illness:
IllnessA:
c
1
(
d
)
=
1218
e
-
0.05
d
IllnessB:
c
2
(
d
)
=
420
e
-
0.125
d
Ravialso finds that ifachildhas
both
illnesses,becauseof the increased trauma to the immune
system, the totaldecrease incells is theproductof the two functions, rather than thesum.
• Writea function thatmodels thedecrease in thenumberofcells ifachild
had
both
illnesses.
PartC
Ravi isworkingwithdatacollectedby researchersallover theworldconcerning
bacteriagrowth indifferentbodiesofwaterwithdifferent temperatures.Thedatacollected is
inKelvin,Celsius,andFahrenheit.The formula toconvertKelvin toCelsius is
T
(
C
)
=
T
(
K
)
-
273.15,
and the formula toconvertCelsius toFahrenheit is
T
(
F
)
=
9
_
5
T
(
C
)
+
32.
• Writeacomposition function thatcanbeused todirectlyconvertKelvin toFahrenheit.
PartD
Johanna isworkingonaproject involvingasteroids stuck in theorbitofaplanet.
The formula forescape velocity is
v
≥
√
2
GM
_
r
,where
v
is thenecessary velocityneeded to
escapeorbit,
G
is thegravitationalconstant,
M
is themassof theplanet,and
r
is the radius
of theplanet.Thegravitationalconstant is6.673
×
10
-
11
.
• If themassof theEarth is5.98
×
10
24
, inkilograms,and theescape velocityneeded for
anasteroid to leaveEarth’sorbit is 11,184metersper second,determine the radiusof
theEarth. (Note:donotworryaboutunits.)
PartE
Johannanext turnsher focus toaproject involving springs.Theperiodofoscillationofa
springcanbe foundusing the formula
T
=
2
π
√
m
_
k
,where
T
is theperiod,
m
is themassof
theoscillatingbody,and
k
isaconstant.
• Writeanequation for themassof theoscillatingbody, in termsof theperiod.
APPLYMATH
Two studentsatauniversityareeach researchassistants. Johanna isaphysics researchassistantand
Ravi isabiology researchassistant.Theyarebothperforming variouscalculationsondatacollected in their labs.
366
|
Chapter5
|
PerformanceTask
Program:
ALG2
Component:
C05_PST
PDF_Proof
Vendor:
Aptara
Grade:
9–12
for Vocabulary
Review Games and key
vocabulary in 13 languages.
Connecting Concepts
New Vocabulary
Review Vocabulary
C07-040A-888482
O
y
x
314
|
Chapter 5
|
Inverses and Radical Functions


















