
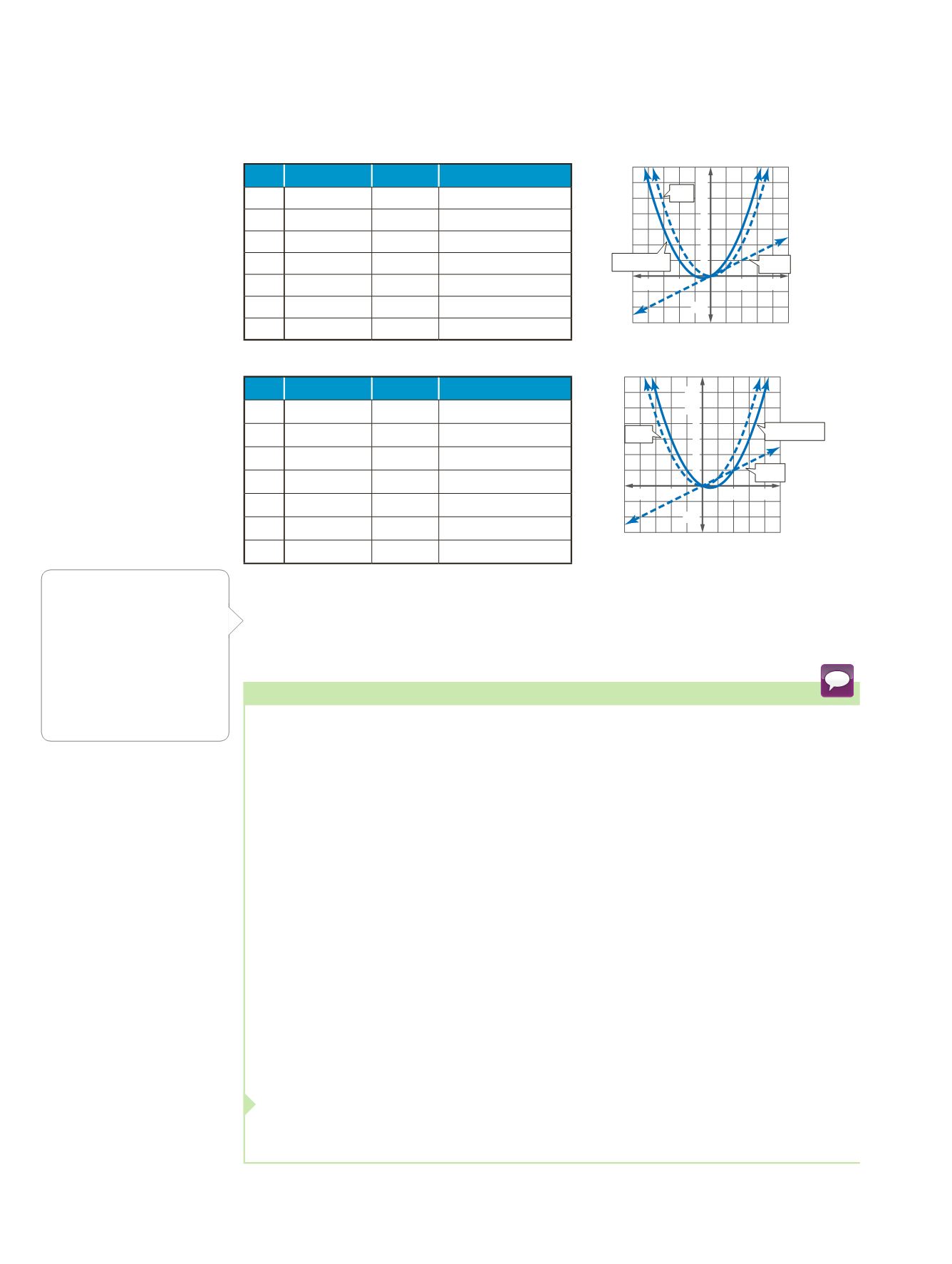
You can graph sum and difference functions by graphing each function involved
separately, then adding their corresponding functional values. Let
f
(
x
)
=
x
2
and
g
(
x
)
=
x
. Examine the graphs of
f
(
x
),
g
(
x
), and their sum and difference.
Find (
f
+
g
)(
x
).
x
f
(
x
)
=
x
2
g
(
x
)
=
x
(
f
+
g)
(
x
)
=
x
2
+
x
-
3
9
-
3
9
+
(
-
3)
=
6
-
2
4
-
2
4
+
(
-
2)
=
2
-
1
1
-
1
1
+
(
-
1)
=
0
0
0
0
0
+
0
=
0
1
1
1
1
+
1
=
2
2
4
2
4
+
2
=
6
3
9
3
9
+
3
=
12
C07-041A-888482
O
−
2
−
4
2 4
y
x
12
10
8
6
4
2
−
4
(
f
+
g
)(
x
)
f
(
x
)
g
(
x
)
Find (
f
-
g
)(
x
).
x
f
(
x
)
=
x
2
g
(
x
)
=
x
(
f
-
g)
(
x
)
=
x
2
-
x
-
3
9
-
3
9
-
(
-
3)
=
12
-
2
4
-
2
4
-
(
-
2)
=
6
-
1
1
-
1
1
-
(
-
1)
=
2
0
0
0
0
-
0
=
0
1
1
1
1
-
1
=
0
2
4
2
4
-
2
=
2
3
9
3
9
-
3
=
6
C07-042A-888482
O
−
2
−
4
2 4
y
x
12
10
8
6
4
2
−
4
f
(
x
)
g
(
x
)
(
f
g
)(
x
)
In Example 1, the functions
f
(
x
) and
g
(
x
) have the same domain of all real numbers. The
functions (
f
+
g
)(
x
) and (
f
-
g
)(
x
) also have domains that include all real numbers. For
each new function, the domain consists of the intersection of the domains of
f
(
x
) and
g
(
x
).
Under division, the domain of the new function is restricted by excluded values that
cause the denominator to equal zero.
Given
f
(
x
)
=
x
2
+
7
x
+
12 and
g
(
x
)
=
3
x
-
4, find each function. Indicate any
restrictions in the domain.
a.
(
f
·
g
)(
x
)
(
f
·
g
)(
x
)
=
f
(
x
)
·
g
(
x
)
Multiplication of functions
=
(
x
2
+
7
x
+
12)(3
x
-
4)
Substitution
=
3
x
3
+
21
x
2
+
36
x
-
4
x
2
-
28
x
-
48
Distributive Property
=
3
x
3
+
17
x
2
+
8
x
-
48
Simplify.
b.
(
f
_
g
)
(
x
)
(
f
_
g
)
(
x
)
=
f
(
x
)
_
g
(
x
)
Division of functions
=
x
2
+
7
x
+
12
__
3
x
-
4
,
x
≠
4
_
3
Substitution
Because
x
=
4
_
3
makes the denominator 3
x
-
4
=
0,
4
_
3
is excluded from the
domain of
(
f
_
g
)
(
x
).
Guided Practice
Given
f
(
x
)
=
x
2
-
7
x
+
2 and
g
(
x
)
=
x
+
4, find each function.
2A.
(
f
·
g
)(
x
)
2B.
(
f
_
g
)
(
x
)
Example 2
Multiply and Divide Functions
Reading Math Tip
intersection
Everyday use—
the intersection of two roads
is where the two roads
meet; Math meaning—the
intersection of two sets is
the set of elements common
to them.
316
|
Lesson 5-1
|
Operations with Functions


















