
Dave Moyer
LESSON 3
Inverse Functions and Relations
1
Find Inverses
Recall that a relation is a set of ordered pairs. The
inverse relation
is
the set of ordered pairs obtained by exchanging the coordinates of each ordered pair.
The domain of a relation becomes the range of its inverse, and the range of the relation
becomes the domain of its inverse.
Key Concept
Inverse Relations
Words
Two relations are inverse relations if and only if whenever one relation contains the
element (
a
,
b
), the other relation contains the element (
b
,
a
).
Example
A
and
B
are inverse relations.
A
= {
(1, 5), (2, 6), (3, 7)
}
B
= {
(5, 1), (6, 2), (7, 3)
}
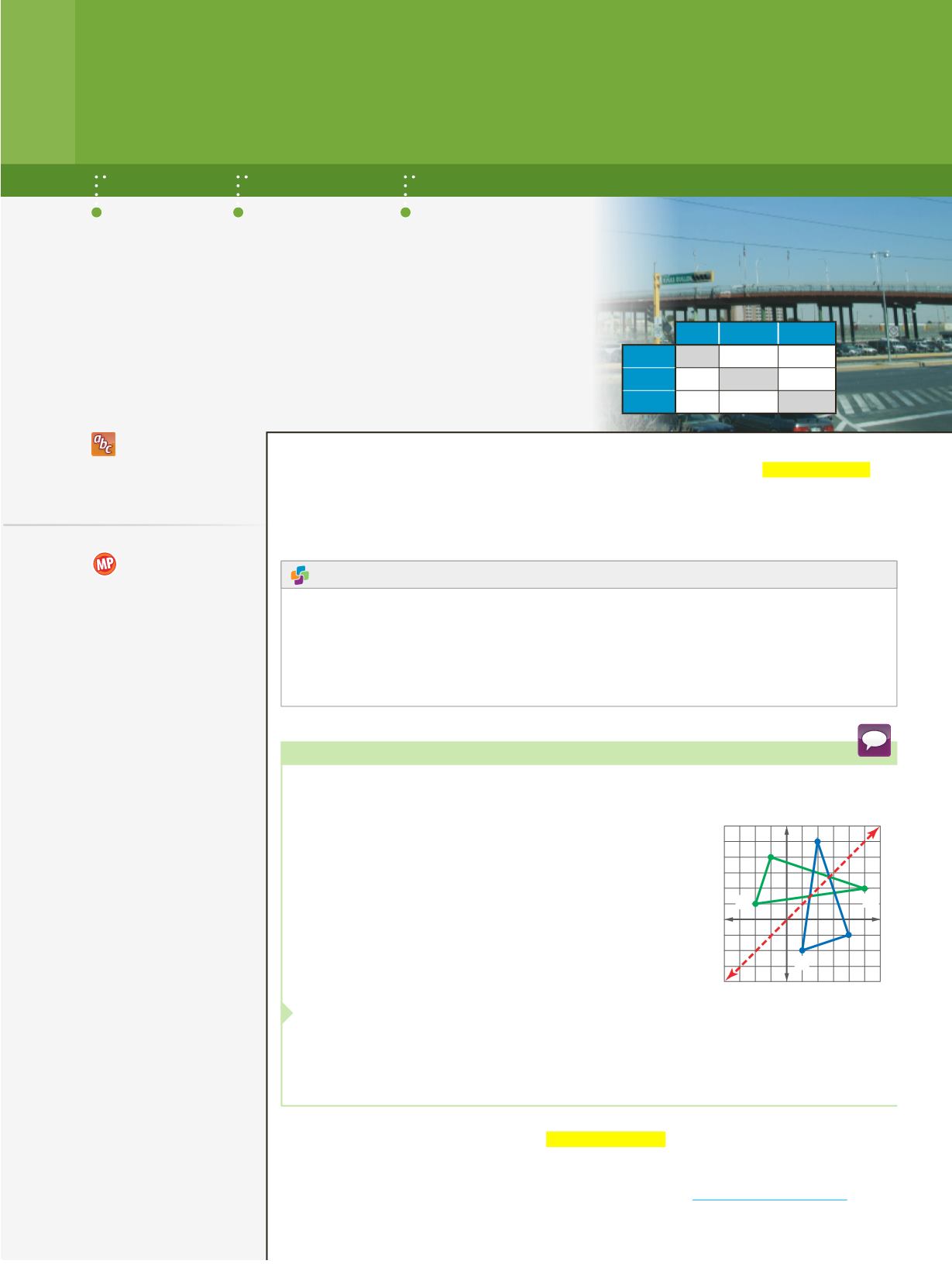
GEOMETRY
The vertices of
△
ABC
can be represented by the relation
{
(1,
-
2),
(2, 5),
(4,
-
1)
}
. Find the inverse of this relation. Describe the graph of the inverse.
Graph the relation. To find the inverse, exchange the
coordinates of the ordered pairs. The inverse of the
relation is
{
(
-
2, 1), (5, 2), (
-
1, 4)
}
.
Plotting these points shows that the ordered pairs
describe the vertices of
△
A
′
B
′
C
′
as a reflection of
△
ABC
in the line
y
=
x
.
Guided Practice
1.
GEOMETRY
The ordered pairs of the relation
{
(
-
8,
-
3), (
-
8,
-
6), (
-
3,
-
6)
}
are the
coordinates of the vertices of a right triangle. Find the inverse of this relation.
Describe the graph of the inverse.
C07-006A-888482
y
x
O
A
'
C
'
B
'
A
C
B
Example 1
Find an Inverse Relation
As with relations, the ordered pairs of
inverse functions
are also related. We can write
the inverse of the function
f
(
x
) as
f
-
1
(
x
).
Why?
The table shows the value of $1 (U.S.)
compared to Canadian dollars and
Mexican pesos.
The equation
p
=
12.45
d
represents
the number of pesos
p
you can
receive for every U.S. dollar
d
. To
determine how many U.S. dollars
you can receive for one Mexican
peso, solve the equation
p
=
12.45
d
for
d
. The result,
d
≈
0.08
p
, is the inverse function.
Now
1
Find the inverse of a
function or relation.
2
Determine whether
two functions or
relations are inverses.
Then
You transformed and
solved equations for
a specific variable.
New
Vocabulary
inverse relation
inverse function
Mathematical
Practices
7
Look for and make use
of structure.
8
Look for and express
regularity in repeated
reasoning.
U.S.
Canada Mexico
U.S.
1.05
12.45
Canada
0.95
11.97
Mexico
0.08 0.08
connectED.mcgraw-hill.com329


















