
Key Concept
Property of Inverses
Words
If
f
and
f
-
1
are inverses, then
f
(
a
)
=
b
if and only if
f
-
1
(
b
)
=
a
.
Example
Let
f
(
x
)
=
x
-
4 and represent its inverse as
f
-
1
(
x
)
=
x
+
4.
Evaluate
f
(6).
Evaluate
f
-
1
(2).
f
(
x
)
=
x
-
4
f
-
1
(
x
)
=
x
+
4
f
(6)
=
6
-
4 or 2
f
-
1
(2)
=
2
+
4 or 6
Because
f
(
x
) and
f
-
1
(
x
) are inverses,
f
(6)
=
2 and
f
-
1
(2)
=
6.
The inverse of a function can be found by exchanging the domain and the range.
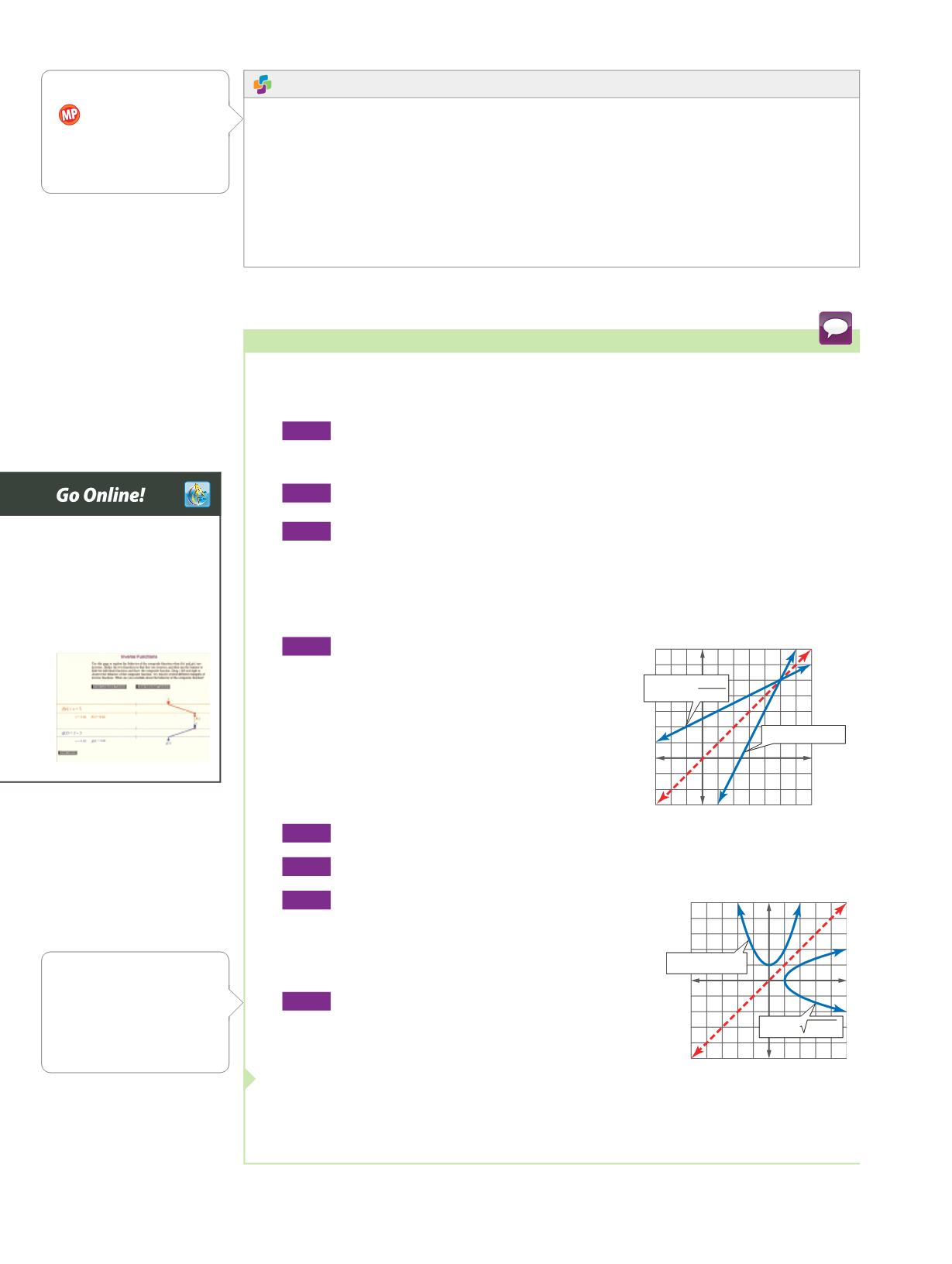
Find the inverse of each function. Then graph the function and its inverse.
a.
f
(
x
)
=
2
x
-
5
Step 1
Rewrite the function as an equation relating
x
and
y
.
f
(
x
)
=
2
x
-
5
→
y
=
2
x
-
5
Step 2
Exchange
x
and
y
in the equation.
x
=
2
y
-
5
Step 3
Solve the equation for
y
.
x
=
2
y
-
5
Inverse of
y
=
2
x
-
5
x
+
5
=
2
y
Add 5 to each side.
x
+
5
_
2
=
y
Divide each side by 2.
Step 4
Replace
y
with
f
-
1
(
x
).
y
=
x
+
5
_
2
→
f
-
1
(
x
)
=
x
+
5
_
2
The inverse of
f
(
x
)
=
2
x
-
5 is
f
-
1
(
x
)
=
x
+
5
_
2
.
The graph of
f
-
1
(
x
)
=
x
+
5
_
2
is the reflection of
the graph of
f
(
x
)
=
2
x
-
5 in the line
y
=
x
.
b.
f
(
x
)
=
x
2
+
1
Step 1
f
(
x
)
=
x
2
+
1
→
y
=
x
2
+
1
Step 2
x
=
y
2
+
1
Step 3
x
=
y
2
+
1
x
-
1
=
y
2
±
√
x
-
1
=
y
Take the square
root of each side.
Step 4
y
= ±
√
x
-
1
Graph
y
= ±
√
x
-
1by reflecting the graph
of
f
(
x
)
=
x
2
+
1 in the line
y
=
x
.
Guided Practice
Find the inverse of each function. Then graph the function and its inverse.
2A.
f
(
x
)
=
x
-
3
_
5
2B.
f
(
x
)
=
3
x
2
Example 2
Find and Graph an Inverse
C07-045A-888482
O
y
x
f
(
x
)
=
x
2
+
1
y
= ±
x
1
C07-007A-888482
y
x
O
f
1
(
x
)
=
x
+
5
2
f
(
x
)
=
2
x
−
5
Reading Math
Sense-Making
f
-
1
is
read
f
inverse
or
the inverse
of f
. Note that
-
1 is
not
an
exponent.
Explore the inverses of
several functions and figure
out when inverse functions
exist and when they don’t
using
The Geometer’s
Sketchpad®
activity in
ConnectED.
Study Tip
Functions
The inverse of
the function in part
b
is not a
function since it does not
pass the vertical line test.
330
|
Lesson 5-3
|
Inverse Functions and Relations


















