
Not all functions have an inverse function. The graph of the initial relation in
Example 2b is a function because it passes the vertical line test. However,
its inverse relation fails this test, so it is not a function. The reflection relationship
between the graph of a function and its inverse relation leads to the horizontal
line test for determining whether an inverse of a function is itself a function.
Key Concept
Horizontal Line Test
Words
A function
f
has an inverse function
f
-
1
if and only
if each horizontal line intersects the graph of the
function in at most one point.
Example
Because no horizontal line intersects the graph
of
f
more than once, the inverse function
f
-
1
exists.
C06_002A_139256
y
=
f
(
x
)
y
x
O
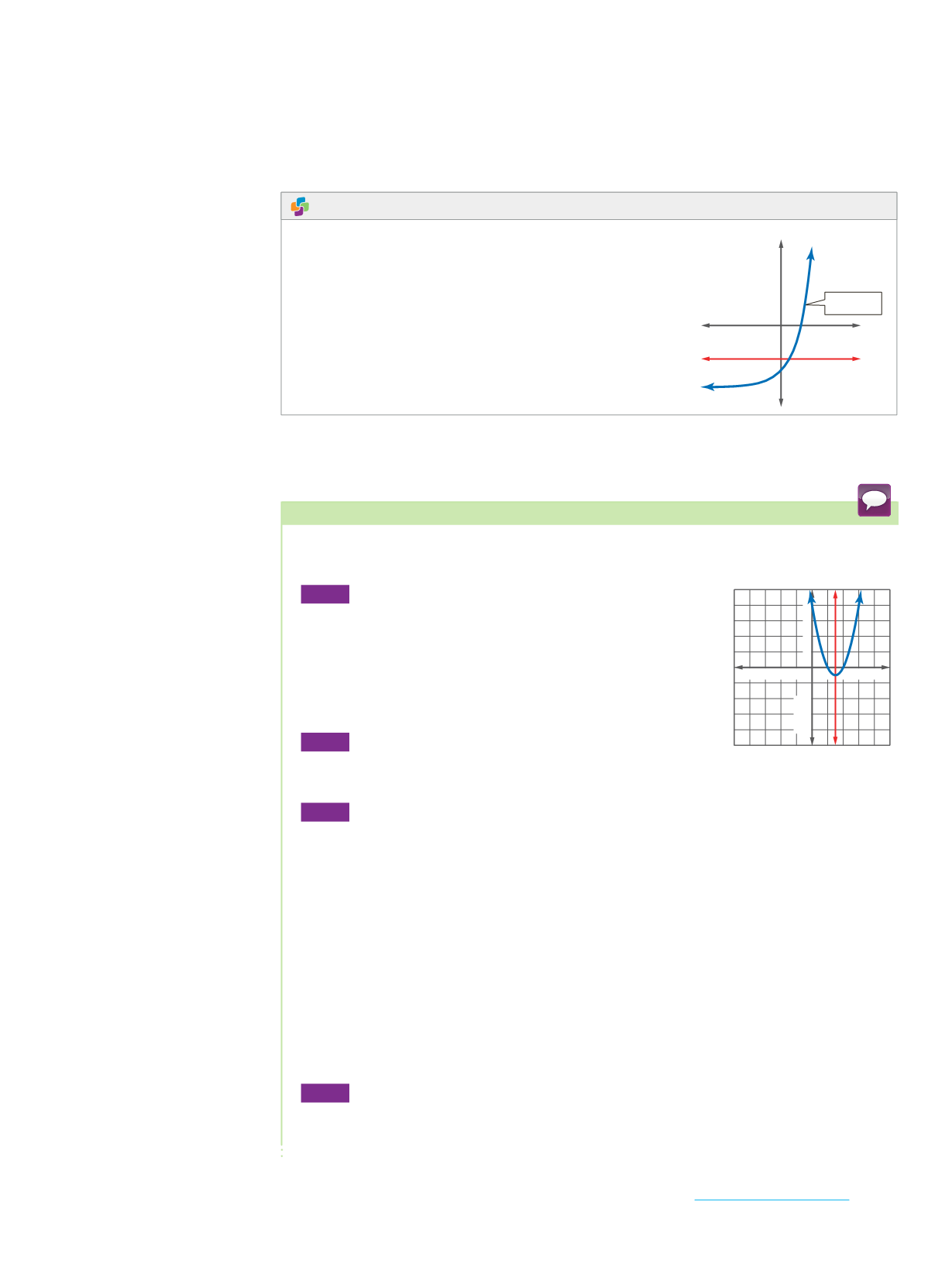
Sometimes it is necessary to restrict the domain of a function in order for its inverse
to be a function.
Example 3
Inverses with Restricted Domains
Find the inverse of
f
(
x
)
=
x
2
-
6
x
+
8. Then graph the function and its inverse.
If necessary, restrict the domain of
f
(
x
) so that the inverse is a function.
Step 1
Use a graph to determine whether
f
(
x
) and
f
-
1
(
x
)
are functions.
f
(
x
) is a function because it passes the vertical line
test. However,
f
(
x
) does not pass the horizontal
line text, which indicates that
f
-
1
(
x
) is not
a function.
Step 2
Identify the axis of symmetry.
The axis of symmetry is
x
=
3.
Step 3
Find
f
-
1
(
x
).
f
(
x
)
=
x
2
-
6
x
+
8
Original function
y
=
x
2
-
6
x
+
8
Replace
f
(
x
) with
y
.
x
=
y
2
-
6
y
+
8
Exchange
x
and
y
.
x
-
8
+
9
=
y
-
6
y
+
9
Complete the square.
x
+
1
=
(
y
-
3)
2
Simplify.
±
√
x
+
1
=
y
-
3
Take the square root of each side.
3
±
√
x
+
1
=
y
Add 3 to each side.
f
-
1
(
x
)
=
3
±
√
x
+
1
Replace
y
with
f
-
1
(
x
).
Step 4
Find a restricted domain of
f
(
x
) so that
f
-
1
(
x
) will be a function.
If the domain is restricted to (
-∞
, 3], then the inverse is
f
-
1
(
x
)
=
3
-
√
x
+
1.
If the domain is restricted to [3,
∞
), then the inverse is
f
-
1
(
x
)
=
3
+
√
x
+
1.
C06_003A_139256
−
4
−
6
−
8
−
2
8
6
4
2
2 4 6 8
−
4
−
6
−
8
x
O
y
connectED.mcgraw-hill.com331


















