
Step 5
Graph.
Notice that in each case, the
range of
f
-
1
(
x
) is restricted so
that the graph passes the vertical
line test.
Guided Practice
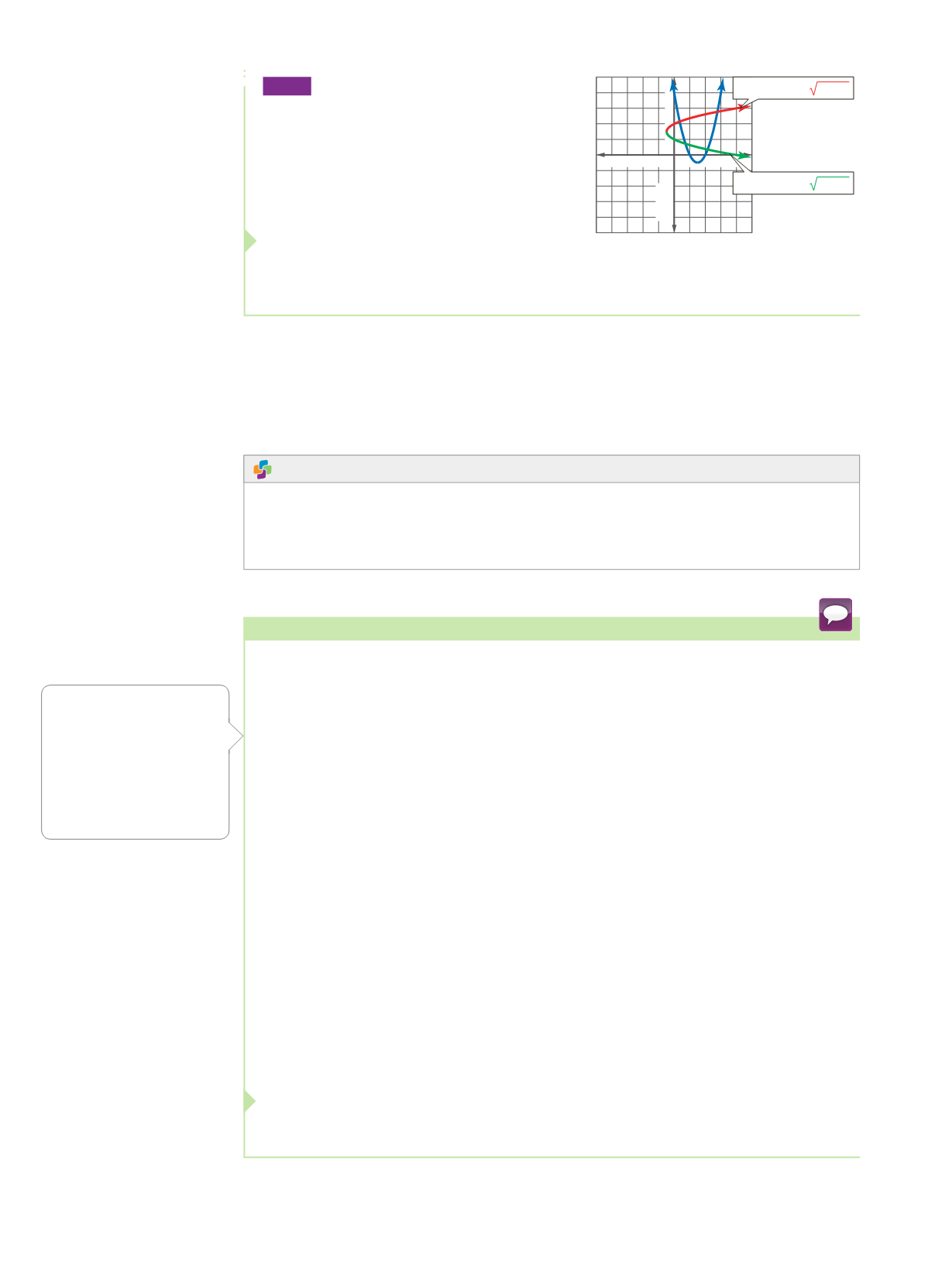
3.
Find the inverse of
f
(
x
)
=
x
2
+
7
x
+
12. Then graph the function and its inverse. If
necessary, restrict the domain of
f
(
x
) so that the inverse is a function.
C06_004A_139256
−
4
−
6
−
8
−
2
8
6
4
2
2 4 6 8
−
4
−
6
−
8
x
O
y
f
1
(
x
)
=
3
+
x
+
1
f
1
(
x
)
=
3
x
+
1
2
Verifying Inverses
You can determine whether two functions are inverses by
finding both of their compositions. If both compositions equal the identity function
I
(
x
)
=
x
, then the functions are inverse functions.
Key Concept
Inverse Functions
Words
Two functions
f
and
g
are inverse functions if and only if both of their compositions
are the identity function.
Symbols
f
(
x
) and
g
(
x
) are inverses if and only if [
f
◦
g
](
x
)
=
x
and [
g
◦
f
](
x
)
=
x
.
Determine whether each pair of functions are inverse functions. Explain
your reasoning.
a.
f
(
x
)
=
3
x
+
9 and
g
(
x
)
=
1
_
3
x
-
3
Verify that the compositions of
f
(
x
) and
g
(
x
) are identity functions.
[
f
◦
g
](
x
)
=
f
[
g
(
x
)]
[
g
◦
f
](
x
)
=
g
[
f
(
x
)]
=
f
(
1
_
3
x
-
3
)
=
g
(3
x
+
9)
=
3
(
1
_
3
x
-
3
)
+
9
=
1
_
3
(3
x
+
9)
-
3
=
x
-
9
+
9 or
x
=
x
+
3
-
3 or
x
The functions are inverses because [
f
◦
g
](
x
)
=
[
g
◦
f
](
x
)
=
x
.
b.
f
(
x
)
=
4
x
2
and
g
(
x
)
=
2
√
x
[
f
◦
g
](
x
)
=
f
(
2
√
x
)
=
4
(
2
√
x
)
2
=
4(4
x
) or 16
x
Because [
f
◦
g
](
x
)
≠
x
,
f
(
x
) and
g
(
x
) are not inverses.
Guided Practice
4A.
f
(
x
)
=
3
x
-
3,
g
(
x
)
=
1
_
3
x
+
4
4B.
f
(
x
)
=
2
x
2
-
1,
g
(
x
)
=
√
x
+
1
_
2
Example 4
Verify that Two Functions are Inverses
Watch Out!
Inverse Functions
Be sure
to check both [
f
◦
g
](
x
) and
[
g
◦
f
](
x
) to verify that
functions are inverses. By
definition, both compositions
must be the identity function.
332
|
Lesson 5-3
|
Inverse Functions and Relations


















